電源を2つ以上持つ回路の解析を簡易化する際、重ね合わせの理論が大変役立ちます。電験三種の試験内容にも、この重ね合わせの定理は頻繁に取り上げられる主要な定理です。本記事では、具体的な例題や問題を交えて、重ね合わせの理論を詳しく解説します。
重ね合わせの理とは?
重ね合わせの理
重ね合わせの理とは、2つ以上の電源を持つ回路において、特定の点での電流や電圧が、各電源が単体で作用した際の合計値と等しいというものです。
わかりやすく説明すると、「電源が2つ以上あるなら、別々の電源として考えると考えやすくなる」という定理です。
この定理を利用すると、全ての電源の中から一つだけを選び、他の電源を取り除いた状態での電流や電圧を計算することができます。そして、この手法を各電源に対して繰り返すことで、元の回路の全体的な電流や電圧を導き出すことが可能となります。
この方法が「重ね合わせ」と名付けられた背景には、各電源による影響が「重ねられる」イメージから来ているといわれています。
キルヒホッフの法則との違い
複数の電源が存在する際、それを単一の電源として扱う理論の一つとして、キルヒホッフの法則が挙げられます。キルヒホッフの第一法則は、接続点での入出電流が等しいという原則を、第二法則は、閉回路内の電源電圧の合計が抵抗の電圧降下の合計と等しいという原則を示しています。
キルヒホッフの法則は実用的で非常に有効ですが、解析する際に連立方程式を設定する必要があるため、計算が複雑になることがあります。しかし、重ね合わせの理論を適用することで、特定の回路ではオームの法則を使用して簡単に解析することが可能です。この理論は主に電流の解析に用いられるものの、電圧の解析にも適用可能です。
重ね合わせの定理を利用する際の注意点として、電圧源を取り除く場合は短絡し、電流源を取り除く場合は開放する必要があります。
結論として、デカルトの言葉「複雑な問題は分割して考察すべき」という考え方が、重ね合わせの理論の核心にピッタリ合っています。
電験3種の理論問題にでてくる重ね合わせ
重ね合わせの理は、電験の理論科目で出てくることがあります。
下は、平成20年の電験3種に出題された問題です。
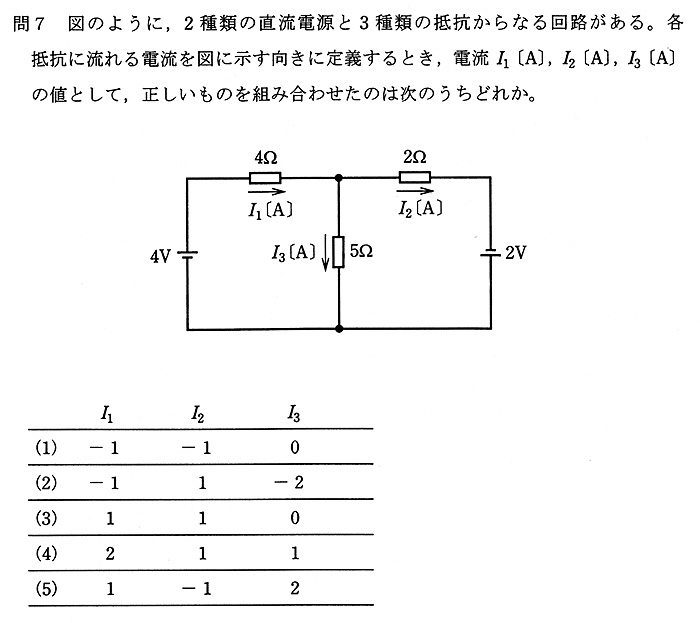
例題
例題1
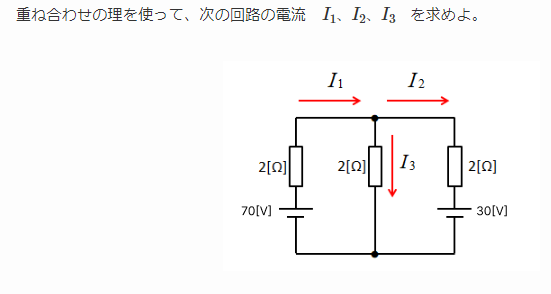
回答1
まず、左側の70Vの電圧源とその周りの2Ωの抵抗に流れる電流 I1を計算します。この部分の回路は独立しているので、オームの法則により
I1=70V/2Ω=35A
次に、右側の30Vの電圧源とその周りの2Ωの抵抗に流れる電流I2を計算します。この部分も独立しているので、オームの法則により
I2=30V/2Ω=15A
中央の2Ωの抵抗に流れる電流 I3は、I1と I3の差として計算されます。これは、左側から流れてくる電流と右側から流れてくる電流の間のバランスを取るためです。
I3=I1-I2=20A
したがって、求める電流は以下になります。
I1= 35A
I2 = 15A
I3 = 20A
例題2
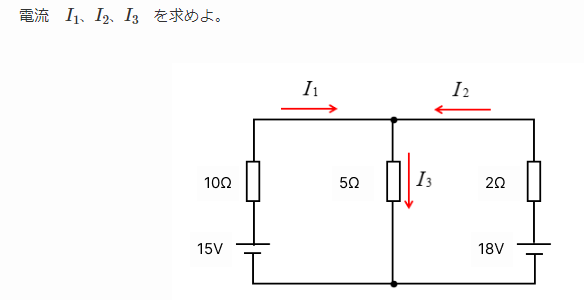
回答2
まず、左側の15Vの電圧源とその周りの10Ωの抵抗に流れる電流 I1 を計算します。この部分の回路は独立しているので、オームの法則により
I1=15V/20=1.5A
次に、右側の18Vの電圧源とその周りの2Ωの抵抗に流れる電流 I2を計算します。この部分も独立しているので、オームの法則により
I2=18V/2=9A
中央の5Ωの抵抗に流れる電流 (I_3) は、(I_1) と (I_2) の差として計算されます。これは、左側から流れてくる電流と右側から流れてくる電流の間のバランスを取るためです。
I3=I1-I2=9A-1.5A=7.5A
したがって、求める電流は以下の通りです。
I1= 1.5A
I2= 9A
I3= 7.5A
まとめ
重ね合わせの理は、電気回路の解析において非常に重要な原理の一つです。複雑な回路でも、一つ一つの電源を独立して考え、その結果を合成することで全体の動作を理解することができます。この原理は、電気電子工学の基礎として学ばれ、特に電験3種の試験においても頻繁に出題されるテーマとなっています。理論だけでなく、実際の問題解決にも役立つため、しっかりと理解しておくことが求められます。
本記事では、重ね合わせの理の基本から、具体的な練習問題までを網羅的に解説しています。電験3種を目指す方はもちろん、電気回路の知識を深めたい全ての方におすすめの内容となっています。
まずは転職エージェントに無料相談してみよう!
転職エージェント目線で、ビルメンや電験の転職にお勧めの転職エージェントをまとめました。
電験3種は試験だけでなく認定で取得することもできます。認定取得が可能な企業についても触れていますので、ぜひ参考にしてみてください。