気工学の世界では、キルヒホッフの法則は不可欠な基礎知識です。特に、電気回路を理解する上で重要な「キルヒホッフの第二法則」について、この記事では詳しく解説します。この法則は、電気回路内での電圧の振る舞いを理解するための鍵となり、電気工学だけでなく、物理学やエンジニアリングの分野においても広く応用されています。
初心者から専門家まで、キルヒホッフの法則の基本から応用までをわかりやすく解説し、電気回路の理解を深めましょう。
キルヒホッフの法則とは?
キルヒホッフの法則は、電気回路を理解するのにとても役立つルールです。この法則は、特に複数の部品がつながった電気回路を見るときに重要です。電気の勉強では、まずオームの法則を学んだ後、このキルヒホッフの法則を学ぶことが多いです。この法則を使うと、電圧や抵抗、電流が回路の中でどう関係しているかを数式で表して、その答えを見つけることができます。
キルヒホッフの法則には、大きく分けて2つの部分があります。一つは、電気回路のある点(節点)に集まる電流の合計についてのルールです。もう一つは、電気が一周する道(閉回路)の中での電圧の合計に関するルールです。この法則は、1845年にドイツの学者グスタフ・キルヒホフによって発見されました。
ここからは2つの法則の詳細をそれぞれ説明します。
キルヒホッフの第一法則
キルヒホッフの第一法則は、「電流の保存の法則」とも呼ばれ、電気回路のある点(節点)に流れ込む電流の合計は、その点から流れ出る電流の合計と等しい、というものです。
これを水の流れに例えてみましょう。想像してみてください、ある分岐点に3つの水道管がつながっているとします。この分岐点には、2つの水道管から水が流れ込み、1つの水道管から水が流れ出ているとしましょう。
キルヒホッフの第一法則によれば、この分岐点に流れ込む水の量の合計は、流れ出る水の量の合計と等しくなります。つまり、2つの水道管から流れ込む水の量を合わせると、それは分岐点から流れ出る水の量と同じになるのです。
これは電気回路においても同じことが言えます。電流は水の流れと似ていて、電子が流れることで電流が生じます。ある節点に複数の電線がつながっているとき、その節点に流れ込む電流の合計は、そこから流れ出る電流の合計と等しくなります。
【公式】キルヒホッフの第一法則
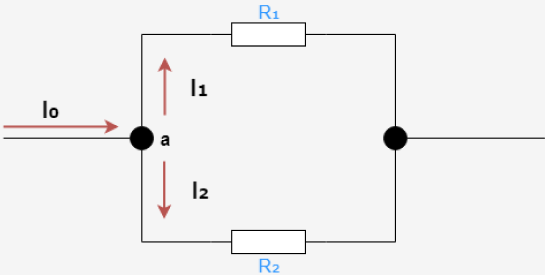
キルヒホッフの第二法則
キルヒホッフの第二法則は、「電圧の和の法則」とも呼ばれ、電気回路の閉じたループ(閉回路)を一周するとき、途中で得た電圧の上昇と下降が合計でゼロになる、というものです。
この法則を山や谷を旅するハイキングに例えてみましょう。あなたが山の麓から出発して、いくつかの山を越えて元の場所に戻るハイキングをするとします。山を登るときは高度を上げ(電圧が上昇)、山を下るときは高度を下げます(電圧が下降)。最終的に元の出発点に戻ったとき、あなたが登った高度と下った高度の合計はゼロになります。つまり、高度の上昇と下降が打ち消し合うのです。
これは電気回路においても同じことが言えます。電圧は高度のようなもので、電気回路の特定のルートを一周するとき、途中で経験する電圧の上昇と下降は合計でゼロになります。これは、電池や抵抗などを通過する際に電圧が上がったり下がったりすることを意味しますが、最終的にはその変化が打ち消し合って、元の電圧に戻るのです。
【公式】キルヒホッフの第二法則
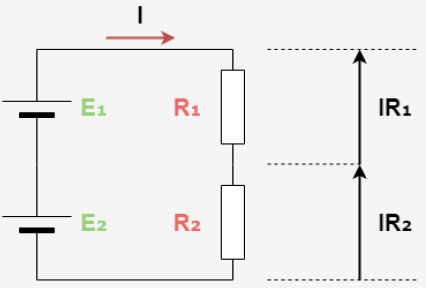
節点、枝、閉回路とは?
キルヒホッフの法則は、電気回路の解析に不可欠なツールです。この法則を理解するためには、回路の「節点」、「枝」、「閉回路」という三つの基本的な概念を把握することが重要です。節点は電流が集まる点、枝は節点間を結ぶ道、閉回路は回路を一周する経路を指します。これらの要素を通じて、キルヒホッフの法則は電気回路内の電流と電圧の振る舞いを明確に説明し、複雑な回路の動作を理解するための鍵となります。
節点
節点とは、電流の分岐や合流が発生する可能性がある点をさします。基準からの電圧が独立したもので、よくa,bといった表現で節点を表します。
枝
枝とは、節点と節点に連結される分岐のない経路のことをいい、枝路ともいいます。電流の分岐や合流がないので、枝は全体を同じ大きさの電流が流れることになります。
閉回路
閉回路とは、回路中のある点から出発し、いくつかの節点と枝を経由し、出発点に戻った際に、そのたどった経路のことです。ループともよばれます。
例題
問題
下の図の電流をI₁、I₂、I₃と仮定し、図4のような直列回路において、抵抗6Ωの端子電圧の大きさVの値を求めよ。
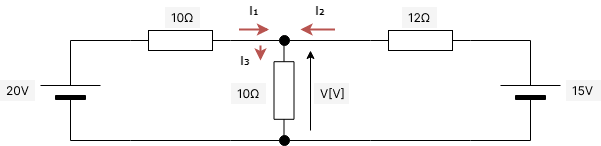
解説
- キルヒホフの第1法則(節点の法則): I₁ + I₂ = I₃ ・・・・・(1)
- キルヒホフの第2法則(ループの法則):
- 閉回路(左): 20V = 10Ω・I₁ + 10Ω・I₃ ・・・・・(2)
- 閉回路(右): 15V = 12Ω・I₂ + 10Ω・I₃ ・・・・・(3)
式(1)から I₁ = I₃ - I₂ を式(2)に代入: 20 = 20I₃ - 10I₂ ・・・・・(4)
式(3)を整理: 10I₃ = 15 - 12I₂ ・・・・・(5)
式(4)と(5)を連立して解く: I₂ = 10 / 34 = 5 / 17 A I₃ = (15 - 12(5/17)) / 10 = 39 / 340 A
10Ωの抵抗の端子電圧 V: V = I₃ × 10Ω = (39 / 340) × 10 = 39 / 34 V ≈ 1.15 V
したがって、求める端子電圧 V は約 1.15 V です。